Esercizi per l'unità 6

Esercizio 1

Scrivere una programma guess che gioca con l'utente. Il gioco consiste nel far indovinare un numero all'utente tramite mosse successive. Il programma inizializza un numero qualsiasi compreso tra 0 e 100. Quindi chiede all'utente di immettere un numero per indovinare quello inizializzato dal programma. Se il numero che l'utente immette è più grande del numero iniziale, il programma deve restituire un messaggio che indica che il numero è più grande, se il numero è più piccolo segnala che il numero ` più piccolo. Se l'utente indovina il numero, un segnale a schermo indica il numero di mosse eseguite. Il programma deve prevedere che l'utente decida di uscire dal gioco prima di indovinare il numero. guess

Scrivere tre programmi java, uno per trovare il minimo tra un insieme di interi tutti strettamente minori di 100. Uno che calcola il minimo tra un insieme di interi che contiene almeno un elemento, ed uno per ottenere il minimo nel caso generale (insieme può essere vuoto e l'intervallo di interi non è limitato). L'insieme di interi deve essere inserito dall'utente. Quando l'utente interrompe di immettere interi viene restituito un messaggio che dice qual'è l'intero minore inmmesso oppure indica che l'insieme ` vuoto. Provare a violare appositamente le considzioni poste nei primi due programmi e osservate cosa accade.

      minimoIntero100       minimoInteroNonVuoto       minimoIntero

Scrivere una programma java che accetti in ingresso una serie di stringhe e stampi la stringa più lunga immessa.

      stringPiuLunga

Esercizio 4

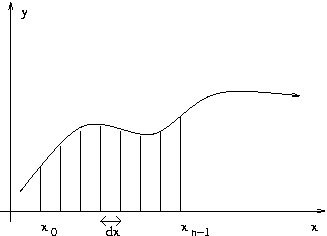
Una funzione campionata è una funzione y=f(x) i cui valori y sono definiti solamente per determinati valori di x (detti punti di campionamento) opportunamente intervallati. In particolare, una funzione campionata è caratterizzata da:

• un punto di campionamento iniziale x0 (un reale)
• un intervallo di campionamento dx (un reale)
• un numero fissato di campioni n (un intero)

e l'i-esimo valore campionato (i = 0,..,n-1) corrisponde al valore della funzione yi = f(xi) dove xi è l'i-esimo punto di campionamento ed è pari a xi=x0+i*dx.

Progettare e realizzare una classe FunzioneCampionata che rappresenti una funzione campionata. In particolare, la funzione di cui interessano i campioni è y = 2*x + 3, mentre il punto di campionamento iniziale, l'intervallo di campionamento e il numero di campioni variano da istanza a istanza.

• un opportuno costruttore;
• metodi che restituiscono il punto di campionamento iniziale, l'intervallo di campionamento e il numero di campioni;
• un metodo puntoCampionamento, che dato un intero i restituisce l'i-esimo punto di campionamento;
• un metodo valoreCampionato, che dato un intero i restituisce l'i-esimo valore campionato;
• un metodo toString, che restituisce una stringa composta da tutte le coppie separate da '\n', formate da punto di campionamento e valore campionato separati da uno spazio.

Soluzione

Esercizio 6

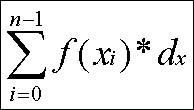
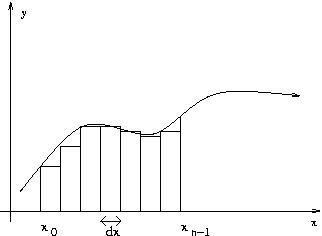
L'area racchiusa tra i rettangoli evidenziati nella figura seguente rappresenta l'integrale di una funzione campionata:

Soluzione

Esercizio 7

Soluzione