grammatiche

valore espressione:

• si parte dal basso
• si compongono 2+3=5
• si fa risalire 5
• poi 5*4=20

valutazione, sull'albero

animazione:

animazione non visualizzabile con questo browser

albero sintattico

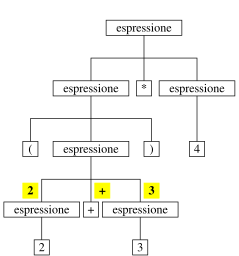
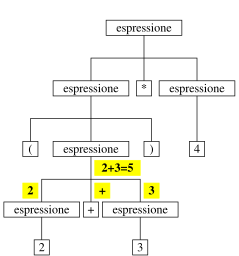
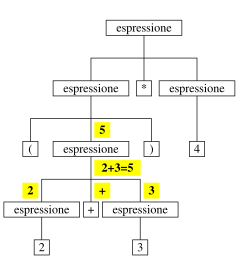
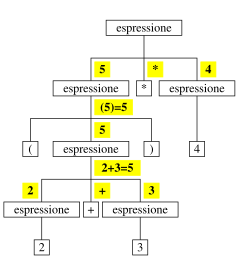
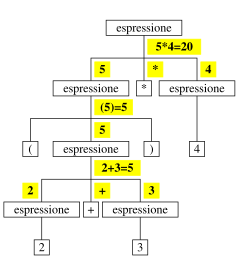
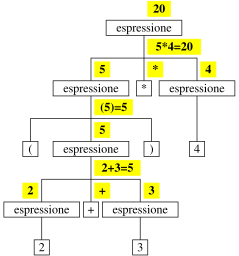
struttura ad albero ottenuta dalla derivazione

derivazione stringa s ⇒ albero sintattico di s

albero di s in questa grammatica
con un'altra grammatica può essere diverso

derivazioni diverse

2+3*4 senza le parentesi
si può ottenere in due modi diversi

                     espressione
                          |
             +------------+------------+
             |            |            |
        espressione       *       espressione
             |                         |
     +-------+-------+                 |
     |       |       |                 |
espressione  +  espressione            4
     |               |
     |               |
     2               3

              espressione
                   |
     +-------------+-------------+
     |             |             |
espressione        +        espressione
     |                           |
     |                   +-------+-------+
     |                   |       |       |
     2              espressione  *  espressione
                         |               |
                         |               |
                         3               4

valutazione nei due casi

                     espressione
                          |
             +------------+------------+
             |            |            |
        espressione       *       espressione
             |                         |
     +-------+-------+                 |
     |       |       |                 |
espressione  +  espressione            4
     |               |
     |               |
     2               3

              espressione
                   |
     +-------------+-------------+
     |             |             |
espressione        +        espressione
     |                           |
     |                   +-------+-------+
     |                   |       |       |
     2              espressione  *  espressione
                         |               |
                         |               |
                         3               4

primo errato
secondo giusto

valutazioni errate

stessa stringa 2+3*4

due alberi diversi

uno dei due dà un valore errato (20)
l'altro corretto (14)

altre stringhe hanno un albero unico: es. 9+3

altre ne hanno diversi, ma tutti corretti: es. 1+2+3

grammatiche ambigue

una grammatica in cui esistono stringhe che hanno più di un albero di derivazione si dice ambigua

esistono stringhe con alberi di derivazione diversi
(altre possono averne uno solo)

problema delle grammatiche ambigue?

problema dell'ambiguità

albero = struttura della stringa

due alberi: qual è la struttura della stringa?

alcune grammatiche si possono rendere non ambigue

espressione numerica: grammatica non ambigua

espressione → espressioneper
espressione → espressionepiu
espressioneper → numero
espressioneper → (espressionepiu)
espressioneper → numero * espressioneper
espressioneper → (espressionepiu) * espressioneper
espressionepiu → numero
espressionepiu → espressioneper
espressionepiu → espressioneper + espressionepiu
numero → cifra
numero → cifra numero
cifra → 0
…
cifra → 9

non ambigua: perchè?

generare qualcosa * qualcosa

espressione → espressioneper
espressione → espressionepiu
espressioneper → numero
espressioneper → (espressionepiu)
espressioneper → numero * espressioneper
espressioneper → (espressionepiu) * espressioneper
espressionepiu → numero
espressionepiu → espressioneper
espressionepiu → espressioneper + espressionepiu
…

unici modi:

• espressione ⇒ espressioneper ⇒ numero * espressioneper
  oppure
• espressione ⇒ espressioneper ⇒ (espressionepiu) * espressioneper

significato?

significato di una derivazione

• espressione ⇒ espressioneper ⇒ numero * espressioneper
  oppure
• espressione ⇒ espressioneper ⇒ (espressionepiu) * espressioneper

a parole: moltiplicazione solo fra:

• numeri
• somma fra parentesi
• altri prodotti

alberi esclusi

2+3*4

non può essere 2+3 moltiplicato per 4

sarebbe una somma senza parentesi moltiplicata per altro

unico albero possibile:
quello di 2 sommato a 3*4

derivazione corretta

unica derivazione possibile di 2+3*4

espressione ⇒
⇒ espressionepiu
⇒ espressioneper + espressionepiu
⇒ numero + espressionepiu
⇒ numero + espressioneper
⇒ numero + numero * espressioneper
⇒ numero + numero * numero 

nessuna altra possibile…

derivazione sbagliata

proviamo a generare 2+3*4 in modo sbagliato
come se fosse 2+3 moltiplicato per 4

espressione ⇒
⇒ espressioneper
⇒ numero * espressioneper
 ???
⇒   2    +    3 * 4

numero può produrre 2
ma dopo dovrebbe esserci *

alternativa…

altra regola

espressione ⇒
⇒ espressioneper
⇒ (espressionepiu) * espressioneper
  ???
⇒    2   +   3     *       4

la stringa finale non ha le parentesi

non si può derivare

derivazioni sbagliate: conclusione

partendo con espressione ⇒ espressionper
non c'è modo di generare 2+3*4

unico modo: partire da espressione ⇒ espressionepiu

significato 2+3*4 è una somma
ok: infatti è 2 sommato a 3*4

grammatiche equivalenti

osservazione:

esistono grammatiche diverse che generano le stesse stringhe

si dicono equivalenti

grammatiche regolari

certe regole non ammesse

equivalenti a espressioni regolari e automi a stati finiti

grammatiche regolari destre

solo regole:

X → a
X → a Y

X e Y: non terminali
a: terminale

esempio: sequenze di cifre

numeri interi positivi

N → 0
N → 1
N → 2
N → 3
N → 4
N → 5
N → 6
N → 7
N → 8
N → 9
N → 0 N
N → 1 N
N → 2 N
N → 3 N
N → 4 N
N → 5 N
N → 6 N
N → 7 N
N → 8 N
N → 9 N

grammatica regolare destra

numeri positivi: esempio di derivazione

N ⇒
⇒ 4 N
⇒ 4 8 N
⇒ 4 8 0

altro esempio di derivazione

N ⇒
⇒ 1 N
⇒ 1 0 N
⇒ 1 0 9 N
⇒ 1 0 9 4 N
⇒ 1 0 9 4 3

grammatiche regolari sinistre

solo regole:

X → a
X → Y a

X e Y: non terminali
a: terminale

grammatiche regolari sinistre: esempio

sempre numeri interi positivi

N → 0
N → 1
N → 2
N → 3
N → 4
N → 5
N → 6
N → 7
N → 8
N → 9
N → N 0
N → N 1
N → N 2
N → N 3
N → N 4
N → N 5
N → N 6
N → N 7
N → N 9
N → N 9

esempio di derivazione

N ⇒
⇒ N 0
⇒ N 8 0
⇒ 4 8 0

stessa sequenza vista prima

generata a partire dal fondo
la grammatica regolare destra la generava a partire dall'inizio

stessi linguaggi

automi deterministici = automi non deterministici = espressioni regolari = grammatiche regolari destre = grammatiche regolari sinistre

significa:

• per ogni automa deterministico
• esiste una grammatica regolare sinistra
  tale che:
  • se una stringa è accettata dall'automa
  • è generata dalla grammatica
  • e viceversa

ecc.

linguaggio

linguaggio = insieme di stringhe

un linguaggio divide le stringhe in:

• appartengono all'insieme
• non appartengono

automi, espressioni, grammatiche: dividono le stringhe

• accettate / non accettate
• collimano / non collimano
• generano / non generano

rappresentano linguaggi

stessi linguaggi

automi deterministici = automi non deterministici = espressioni regolari = grammatiche regolari destre = grammatiche regolari sinistre

significa:

si possono usare per rappresentare gli stessi linguaggi

non tutti i linguaggi si rappresentano in questi modi

linguaggi non regolari

stringhe aaaabbbb con:
tante a quante b

= una sequenza di a seguita da una sequenza di b di lunghezza uguale

non c'è una grammatica regolare che accetta tutte e sole queste stringhe

grammatica regolare: tentativo

qualcosa di simile:

X → a
X → a X
X → b Y
Y → b
Y → b Y

genera per esempio aaaabbbb

ma anche aabbbb

genera stringhe di troppo
non è il linguaggio voluto

con gli altri meccanismi

aⁿ = stringa di a ripetuta n volte

stringhe aⁿbⁿ

dato che grammatica regolare destra = espressioni regolari = …

• non esiste una espressione regolare che collima con tutte e sole le stringhe aⁿbⁿ
• non esiste una automa a stati finiti che accetta tutte e sole le stringhe aⁿbⁿ
• non esiste una gramatica regolare sinistra che genera tutte e sole le stringhe aⁿbⁿ

perchè no?

tentativo con automa:

 0 -b-> (1)
(a)     (b)

  0 -a-> 1 -a-> 3 -a-> 5
        /      /      /
    <-b    <-b    <-b 
(2) <-b- 4 <-b- 6 <-b

perchè no?

tentativo con le espressioni regolari:

• a{n}b{n} il numero n va specificato
  es. a{4}b{4}
• a*b* accetta anche abbbb

grammatica non regolare

X → a b
X → a X b

esempio di derivazione:

X ⇒ a X b ⇒ a a X b b ⇒ a a a X b b b ⇒ a a a a b b b b

non si può riscrivere come una regolare?

espressione regolare equivalente?

ma X → a X b no

al massimo: X → a X

nota su regolari destre e sinistre

non si possono mischiare regole destre e sinistre

es:

X → a Z
Z → X b

non è una grammatica regolare!

regolare destra = regolare sinistra
insieme = come senza nessuna restrizione

esempio più utile

aⁿbⁿ non capita spesso

capita stringhe con elementi a coppie

X → a X b

come dire a -qualcosa- b

esempio: espressioni con parentesi:

X → ( X )

ogni parentesi aperta ha la sua chiusa
e viceversa

delimitatori

generalizzazione delle parentesi

forma apertura -qualcosa- chiusura

esempio: parentesi aperta e chiusa

altro esempio: html

delimitatori in html, xml, svg, ecc.

esempio: tabella html:

<table> celle-della-tabella </table>

all'interno di una cella si può mettere un'altra tabella:

<table> celle <table> celle-sottotabella </table> celle </table>

quasi tutte le pagine web attualmente esistenti usa questo genere di struttura a tabelle l'una dentro l'altra per disporre le loro parti nelle posizioni volute

tabelle, con grammatiche non regolari

testo → <table> contenutotabella </table>
contenutotabella → … testo …

delimitatori simmetrici, in generale

A → aperto B chiuso

le stringhe generate hanno sempre aperto e chiuso bilanciati

tipi di grammatiche

finora:

• nonterminale → terminale nonterminale
  regolare destra
• nonterminale → nonterminale terminale
  regolare sinistra
• nonterminale → sequenza
  forma più generale vista finora

esiste una forma ancora più generale

grammatiche generali

non terminale → sequenza

grammatica non contestuale
quelle viste finora

sequenza → sequenza

grammatiche a struttura di frase

forma più generale possibile

c'è un vincolo su sequenza → sequenza

grammatiche a struttura di frase

sequenza → sequenza

vincolo:

la sequenza prima di → deve contenere almeno un simbolo non terminale

sequenza di terminali: non si può modificare

tutte la altre: sì

esempi di regole generali

XaYb → Zcd
aXbWz → arcbWz

se in una sequenza compare XaYb
al suo posto si può mettere Zcd

anche se a e b sono terminali!

classificazione delle grammatiche

sequenza X sequenza → sequenza

grammatiche a struttura di frase

sequenza1 X sequenza2 → sequenza1 sequenza sequenza2

grammatiche contestuali

X → sequenza

grammatiche non contestuali

X → a Y

grammatiche regolari destre
(sinistre: simili)

X non terminale, a terminale

grammatiche contestuali

intermedie fra struttura di frase e non contestuali

seq1 X seq2 → seq1 sequenza seq2

• non generale come le grammatiche a struttura di frase
  solo X si può rimpiazzare
• più generali delle non contestuali
  si può imporre che X si rimpiazza solo se è in un certo contesto

contesto = quello che c'è prima e dopo
(seq1 prima e seq2 dopo)

contestuali e non contestuali

regole simili:

contestuale

acXdb → acZwYdb

non contestuale

X → ZwY

primo caso: X → ZwY si può applicare solo se prima di X c'è ac e dopo db

secondo caso: si può applicare sempre

forma di Backus-Naur

modo compatto di scrivere grammatiche non contestuali

si usano alcuni operatori delle espressioni regolari

BNF=Backus-Naur Form

BNF: alternativa

espr → numero
espr → (espr)
espr → espr * espr
espr → espr + espr

in BNF diventa:

espr → numero | (espr) | espr * espr | espr + espr

vantaggi…

vantaggi della condensazione

espr → numero | (espr) | espr * espr | espr + espr

• più compatta
• anche più facile da leggere

intuitivo: espr è numero oppure espressione fra parentesi, oppure…

forma estesa: bisognava leggere tutte le regole espr → … per capirlo

forma di Backus-Naur estesa (EBFN)

usa altre cose prese dalle espressioni regolari

ripetizione, in modo esteso:

numero → cifra
numero → cifra numero

• poco intuitivo
• richiede due regole ogni volta

EBNF: ripetizione

numero → cifra {cifra}

qui graffe = ripetizione anche vuota

quindi {cifra} = zero o più cifre

come * delle espressioni regolari

regola molto più facile da leggere

EBNF: opzionalità

invece di ? si usano le parentesi quadre:

numeroconsegno → [-] numero

intero con segno

forma estesa:

numeroconsegno → numero
numeroconsegno → - numero

EBNF: altro

parentesi ( ) come nelle espressioni regolari

al posto di → si usa =
oppure :==

EBNF: classificazione

sempre grammatiche non contestuali

solo una forma più semplice e intuitiva

EBNF: esempio

messaggi scambiati nel protocollo HTTP

esempio: URL

http_URL = "http:" "//" host [ ":" port ] [ abs_path [ "?" query ]]

variante di EBNF
"…" = stringa da interpretare letteralmente

EBNF: esempio più complesso

sempre in HTTP

nel protocollo viene passata la data

HTTP-date    = rfc1123-date | rfc850-date | asctime-date
rfc1123-date = wkday "," SP date1 SP time SP "GMT"
rfc850-date  = weekday "," SP date2 SP time SP "GMT"
asctime-date = wkday SP date3 SP time SP 4DIGIT
date1        = 2DIGIT SP month SP 4DIGIT
               ; day month year (e.g., 02 Jun 1982)
date2        = 2DIGIT "-" month "-" 2DIGIT
               ; day-month-year (e.g., 02-Jun-82)
date3        = month SP ( 2DIGIT | ( SP 1DIGIT ))
               ; month day (e.g., Jun  2)
time         = 2DIGIT ":" 2DIGIT ":" 2DIGIT
               ; 00:00:00 - 23:59:59
wkday        = "Mon" | "Tue" | "Wed"
             | "Thu" | "Fri" | "Sat" | "Sun"
weekday      = "Monday" | "Tuesday" | "Wednesday"
             | "Thursday" | "Friday" | "Saturday" | "Sunday"
month        = "Jan" | "Feb" | "Mar" | "Apr"
             | "May" | "Jun" | "Jul" | "Aug"
             | "Sep" | "Oct" | "Nov" | "Dec"

definiti altrove: SP (spazio)
1DIGIT, 2DIGIT

; indica l'inizio di un commento

EBNF: altro esempio

commenti in html e xml:

Comment ::= '<!--' ((Char - '-') | ('-' (Char - '-')))* '-->'

' per indicare stringhe letterali

Char - '-' = qualsiasi carattere tranne -

esempio:

<!-- questo e' un commento -->

EBNF: grammatica Python

…
compound_stmt: if_stmt | while_stmt | for_stmt | try_stmt | with_stmt | funcdef
if_stmt: 'if' test ':' suite ('elif' test ':' suite)* ['else' ':' suite]
while_stmt: 'while' test ':' suite ['else' ':' suite]
for_stmt: 'for' exprlist 'in' testlist ':' suite ['else' ':' suite]
…

: al posto di →

* per indicare la ripetizione

EBNF: varianti

cose comuni:

• "…" o '…' per indicare stringhe da prendere in modo letterale
  (sequenze di simboli terminali)
• | per indicare l'alternativa
• […] per indicare l'opzionalità

analisi top-down

dice se una stringa si può generare da una grammatica

si parte dal simbolo iniziale

a ogni passo si cerca di capire quale regola applicare

si guardano uno o più caratteri della stringa

top-down: esempio

grammatica:

espr → par
espr → espr * espr
espr → espr + espr
par → 1
par → ( espr )

stringa 1*(1+1)

top-down: esempio

grammatica:

espr → par
espr → espr * espr
espr → espr + espr
par → 1
par → ( espr )

stringa 1*(1+1)

inizio: espr

applico una regola espr → …

quale?

top-down: esempio

grammatica:

espr → par
espr → espr * espr
espr → espr + espr
par → 1
par → ( espr )

stringa 1*(1+1)

quale regola espr → … applico?

guardando solo il primo 1:

non lo so
tutte e tre le espr → … generano stringhe che iniziano con 1

guardando 1*:

regola espr → espr * espr

poi: la prima espr diventa par che diventa 1

ecc.

grammatiche LL(1)

si capisce cosa applicare guardando solo il primo carattere

grammatica di prima: non è LL(1)

si può modificare per renderla tale

versione LL(1)

genera le stesse stringhe:

espr → par seg
par → 1
par → ( espr )
seg → ε
seg → + espr
seg → * espr

ε = stringa vuota

ora: analisi

primo passo: tabella

non terminale/terminale → regola da applicare

tabella

cosa significa?

tabella: esempio

la prima cella dice che:

da espr, per generare una stringa che inizia con 1, occorre applicare espr → par seg

cella di riga espr e colonna 1: contiene par seg

celle vuote

da seg non c'è modo di generare una stringa che inizia con (

lo stesso per le altre celle con -

tabella: ε

da seg forse si può generare ) altro

ma solo applicando seg → ε

tabella: ultima colonna

ultima colonna: cosa fare se la stringa è finita

• - della prima riga = espr non può generare ε
• ε della terza riga: = seg può generare ε

tabella: generazione

derivare questa tabella in generale non è semplice

ci sono varie complicazioni

esempio di analisi

stringa di esempio: 1*(1+1)

in ogni momento: pila + resto della stringa

inizio:

espr

1+(1*1)

elemento in cima + primo della stringa: tabella

passo 1

I → S
I → D
S → ab
S → aSb
D → abb
D → aDbb

if a==b:
    print 'abcd'
    print 'print'

print '    = afi: ='
print
print 'a b c d '