




sistema per dire se una stringa è fatta in un certo modo
come per le espressioni regolari:
spiegazione…
[ab]c*(abc|dd)
0 -a-> 1 -a-> 2 -b-> 3 -c-> ((4)) -b-> (c) -d-> 5 -d-------->
cerchietti = stati in cui può trovarsi l'automa
se alla fine della stringa ci si trova in uno stato con doppio cerchio la stringa è accettata
automi = espressioni regolari
(automa accetta se e solo se espressione collima)
automa:
funzionamento…
accettazione/rifiuto:
automa di prima
stringa 'accabc'
[]
fine stringa → stato finale
stringa accettata
stringa 'aacb'
[]
no uscita da stato → stringa rifiutata
stringa 'bcab'
[]
ultimo stato non doppio → stringa rifiutata
due possibili motivi:
0 --ae-> [1] (bcd) <-bcd- (ae)
accetta le stringhe che:
uguale all'espressione regolare ^[abcde]*[ae]$
arco con più lettere: seguire per una qualsiasi di queste
cappi = archi che portano allo stesso stato
0 --ae-> [1] (bcd) <-bcd- (ae)
non vuol dire che non si può andare oltre
qui: da 1 (finale) si va in 0
stato finale = se si finisce lì la stringa è accettata
ingresso: monete da 5 e 10 centesimi
eroga con almeno 15 centesimi
non accetta monete successive
niente resto
omesso: ricomincia dall'inizio dopo l'erogazione
+------------+ +--------+ +-----------+ | rilevatore | --> | automa | --> | erogatore | | monete | +--------+ | caffe' | +------------+ +-----------+
-----10c----->
0 -5c-> 1 -5c-> 2 -5c--> (3)
-----10c----> -10c->
stati: indicano i centesimi inseriti
stati finali: abbastanza centesimi per il caffè
nessuno stato successivo a quelli finali:
non accetta successive monete quando bastano
niente resto
più avanti: automa con resto
esempio:
automa che accetta le stringhe che hanno il terzo carattere uguale al primo
serve "memorizzare" il primo carattere
stato-memoria = stati diversi a seconda del primo carattere
realizzare l'automa che accetta quasiasi stringa in cui il primo carattere è uguale al terzo
caratteri a, b, c
0 -a-> 1 -*-> 2 -a-> [3] ()* -b-> 4 -*-> 5 -b-> [6] ()* -c-> 7 -*-> 8 -c-> [9) ()*
* = qualsiasi carattere
in questo caso: uguale ad a,b,c
primo carattere a → stato 1
da qui: 2 per forza
se arriva a: stato finale
ma: a in 5 o 8 → rifiuto
cicli su stati finali: va bene qualsiasi cosa arrivi dopo
caratteri 0 e 1
accetta sequenza se: valore numerico > 4
es: accetta 101 e 1000
rifiuta 100, rifiuta 11
(01)
0 -1-> 1 -1-> 2 -01-> (3)
(0) -0-> 4 -1-> (5) (01)
-0-> 6 -01-> 7
(01)
spiegazione?
(01)
0 -1-> 1 -1-> 2 -01-> (3)
(0) -0-> 4 -1-> (5) (01)
-0-> 6 -01-> 7
(01)
zeri iniziali non cambiano il valore: cappio
diramazione ad albero
stringa che rappresenta valore >4: accetta
caratteri successivi: il valore aumenta
(sempre stato finale)
stringhe di lettere {a,b,c,d}
accettare solo stringhe con lettere in ordine
accetta per esempio aaaaa, accetta bbbcccc e abcd e aaaddd
non accetta aaaba e nemmeno abcda
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
ottenuto come?
stato = condizione sulla sequenza arrivata finora
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
in questo caso:
stato 0 = lettere arrivate finora in ordine, ultima a
stato 1 = lettere arrivate finora in ordine, ultima b
stato 2 = lettere arrivate finora in ordine, ultima c
stato 3 = lettere arrivate finora in ordine, ultima d
dice dove andare
stato 2 = lettere arrivate finora in ordine, ultima c
prossimo stato:
deriva dalla definizione di stato…
es: stato 2, arriva d:
quindi: prossimo stato 3
assumendo una certa condizione vera (es. lo stato indica l'ultimo carattere di una sequenza in ordine), si fa in modo tale che all'arrivo del successivo carattere la condizione sia ancora vera
per induzione, la condizione è sempre vera
in generale: condizione = definizione dello stato
c s → q
non possono mancare archi uscenti
si introduce un singolo stato non finale p
se da s manca l'arco con c, se ne mette uno che va in p
p ha un cappio per tutti i caratteri
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
nuovo stato 4
qui vanno gli archi mancanti:
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
| | |
a a,b a,b,c
| | |
| | V
| +-----> 4 (a,b,c)
| ^
+-----------------+
dati: stato e carattere
calcola: stato successivo
sempre definita (automa modificato)
tabella: una riga per ogni stato e carattere
| stato | carattere | successivo |
|---|---|---|
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
| | |
a a,b a,b,c
| | |
| | V
| +-----> 4 (a,b,c)
| ^
+-----------------+
es: da 1 con ingresso d si va in 3
riga:
| stato | carattere | successivo |
|---|---|---|
| … | ||
| 1 | d | 3 |
| … |
una riga per ogni stato e ogni carattere
|
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
| | |
a a,b a,b,c
| | |
| | V
| +-----> 4 (a,b,c)
| ^
+-----------------+
|
da 0 con a si va in 0
da 0 con b si va in 1
ecc.
stati 0,1,2,3,4
servono tre bit
caratteri a,b,c,d
bastano due bit:
0,1,2,3,4 e a,b,c,d si mettono in binario
|
→ |
|
| st | car | succ | |
|---|---|---|---|
| 000 | 00 | → | 000 |
| 000 | 01 | → | 001 |
| 000 | 10 | → | 010 |
| 000 | 11 | → | 011 |
| 001 | 00 | → | 100 |
| 001 | 01 | → | 001 |
| 001 | 10 | → | 010 |
| … | … | … |
ogni bit di succ si sintetizza con un circuito
es: si tiene solo il primo bit
|
→ |
|
sintesi primo bit: si tolgono il secondo e il terzo da succ
sintesi primo bit: si tolgono il secondo e il terzo da succ
resta una tabella con una uscita
solito sistema:
accetta=1, rifiuta=0
| st | finale | |
|---|---|---|
| 000 | → | 1 |
| 001 | → | 1 |
| 010 | → | 1 |
| 011 | → | 1 |
| 100 | → | 0 |
per ogni stato, dice se è finale
sintesi: righe 1, ecc.
+----+
in ------+ SS |
+---+ +---+
| +----+ |
| |
+---------------+
| |
+--------------+ |
| |
| +-----+ | +-----+
+----+ MEM +------+-----+ ACC +----- out
+-----+ +-----+
memoria=?
devo memorizzare tre bit (lo stato)
tre flip-flop
+----+
-----| |-----
+--|> |
| +----+
|
| +----+
-----| |-----
+--|> |
| +----+
|
| +----+
-----| |-----
+--|> |
| +----+
|
clk
clk = clock
dice quando memorizzare lo stato successivo
versione software
una variabile per lo stato
si guarda un carattere per volta
stato="0"
stringa="acccdd"
for input in stringa:
# stato 0
if stato == '0':
if input == 'a':
stato='0'
elif input == 'b':
stato='1'
…
if stato!='4':
print 'stringa accettata'
else:
print 'stringa rifiutata'
stato="0"
stringa="acccdd"
for input in stringa:
print 'stato: ' + stato
print 'in: ' + input
# stato 0
if stato == '0':
if input == 'a':
stato='0'
elif input == 'b':
stato='1'
elif input == 'c':
stato='2'
elif input == 'd':
stato='3'
# stato 1
if stato == '1':
if input == 'a':
stato='4'
elif input == 'b':
stato='1'
elif input == 'c':
stato='2'
elif input == 'd':
stato='3'
# stato 2
if stato == '2':
if input == 'a':
stato='4'
elif input == 'b':
stato='4'
elif input == 'c':
stato='2'
elif input == 'd':
stato='3'
# stato 3
if stato == '3':
if input == 'a':
stato='4'
elif input == 'b':
stato='4'
elif input == 'c':
stato='4'
elif input == 'd':
stato='3'
# stato 4
if stato == '4':
if input == 'a':
stato='4'
elif input == 'b':
stato='4'
elif input == 'c':
stato='4'
elif input == 'd':
stato='4'
print "nuovo stato: "+stato
print '----'
if stato!='4':
print 'stringa accettata'
else:
print 'stringa rifiutata'
stato="0"
stringa="acccdd"
for input in stringa:
print 'stato: ' + stato
print 'in: ' + input
stato={
# stato 0
'0a': '0',
'0b': '1',
'0c': '2',
'0d': '3',
# stato 1
'1a': '4',
'1b': '1',
'1c': '2',
'1d': '3',
# stato 2
'2a': '4',
'2b': '4',
'2c': '2',
'2d': '3',
# stato 3
'3a': '4',
'3b': '4',
'3c': '4',
'3d': '3',
# stato 4
'4a': '4',
'4b': '4',
'4c': '4',
'4d': '4'
}[stato+input]
print "nuovo stato: "+stato
print '----'
if stato!='4':
print 'stringa accettata'
else:
print 'stringa rifiutata'
in termini matematici
serve per dimostrazioni, ecc.
poi: stato iniziale, stati successivi, stati finali
esempi:
insieme di tutti gli stati: S
stato iniziale:
s0 è un elemento di S
stati finali (doppio cerchio):
A è un sottoinsieme di S
dal punto di vista matematico:
s∈S e A⊆S
|
caratteri in ordine:
S={0,1,2,3} s0=0 tutti stati finali: A={0,1,2,3} |
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
|
|
|
valore > quattro:
S={0,1,2,3,4,5,6,7} s0=0 stati finali: A={3,5,7} |
(01)
0 -1-> 1 -1-> 2 -01-> (3)
(0) -0-> 4 -1-> (5) (01)
-0-> 6 -01-> 7
(01)
|
stato iniziale = quello da cui si parte
stati finali = quelli con il doppio cerchio
da stato s e ingresso i si passa a un nuovo stato
è una funzione matematica:
N : S × I → S
permette di calcolare lo stato successivo
N(s,i)=s' vuol dire:
se in s arriva i, si va in s'
+-----d------------+
+-----d--------------------+ |
| +---c------------+ | |
| | | V V V
(0) -b-> (1) -c-> (2) -d-> (3)
(a) (b) (c) (d)
da 0 con c si va in 2
quindi: N(0,c)=2
e poi:
N(2,d)=3 N(0,a)=0 N(3,a) indefinito ecc.
N : S × I → S
dati s e i fornisce lo stato successivo N(s,i)
anche la tabella:
| stato | carattere | successivo |
|---|---|---|
| 0 | a | 0 |
| 0 | b | 1 |
| 0 | c | 2 |
| 0 | d | 3 |
| 1 | a | 4 |
| 1 | b | 1 |
| 1 | c | 2 |
| … | … | … |
si guarda la riga con s e i
la terza casella della riga è lo stato successivo
sono di fatto la stessa cosa
un automa è una quintupla ⟨I, S, s0, N, A⟩
già quasi tutto definito in termini di:
tranne: funzione di stato successivo
prodotto cartesiano:
S×I×S = insieme di triple ⟨s,i,s'⟩ con s∈S, i∈I e s'∈S
funzione (parzialmente definita):
N:S×I→S = sottoinsieme di S×I×S
tale che due terne non hanno gli stessi primi due elementi
intuitivamente: ⟨s,i,s'⟩ se N(s,i)=s'
serve dopo, per definire gli automi non deterministici
stringa c1c2 … cn-1cn
porta allo stato:
N(N(N( … N(N(s0,c1),c2) … ),cn-1),cn)
complicato?
carattere ci → applicare N(…,ci)
N(N(N( … N(N(s0,c1),c2) … ),cn-1),cn)
N(N(N( … N(N(s0,c1),c2) … ),cn-1),cn)
se questo è uno stato finale, la stringa c1c2 … cn-1cn è accettata
altrimenti è rifiutata
c1c2 … cn-1cn accettata se e solo se N(N(N( … N(N(s0,c1),c2) … ),cn-1),cn) ∈ A
N non contiene due triple ⟨s,i,s'⟩ con gli stessi s e i
⟨s,i,s'⟩ ∈ N vuol dire:
da stato s con ingresso i si va a stato s'
no due triple con stessi s e i → stato successivo unico
più triple con stessi s e i → più stati successivi
stando in uno stato, arriva un carattere: si può andare in più stati successivi
cioè, 'nche senso?
sempre con un singolo carattere di input
(a) -ad-> 2
-ac-> 1 -ac-> 3
0* \-d->
-ab-> 4 -d-> 5
-d-> (6)
si inizia in 0
arriva a
si può andare in 1 oppure in 4
dove vado?
non determinismo: dove vado?
(a) -ad-> 2
-Ac-> 1 -ac-> 3
0* \-d->
-Ab-> 4 -d-> 5
-d-> (6)
da 0 con a: vado in 1 o in 4?
si fanno entrambe le scelte
si finisce in 1 e in 4 insieme
(a) -ad-> 2
-ac->*1 -ac-> 3
0 \d->
-ab->*4 -d-> 5
-d-> (6)
vado in 1 e anche in 4
ora arriva d
(a) -aD-> 2
-ac->*1 -ac-> 3
0 \D->
-ab->*4 -D-> 5
-D-> (6)
sono in 1 e 4
con d posso andare:
vado in tutti questi
(a) -aD-> 2
-ac->*1 -ac-> 3
0 \D->
-ab->*4 -D-> 5
-D-> (6)
arrivo in 2, 5 e 6
uno di questi è finale → stringa accettata
(a) -ad-> 2
-ac-> 1 -ac-> 3
0 \d->
-ab-> 4 -c-> 5
-d-> (6)
(animazione)
esempio: stringa ad
vanno considerate tutte le possibilità
si arriva in 2, 5 e 6
6 finale → stringa ad accettata





(a) -ad-> 2
-ac-> 1 -ac-> 3
0 \d->
-ab-> 4 -c-> 5
-d-> (6)
non scelgo niente: sono sistemi teorici
si considerano tutte le possibilità
con ad si arriva in 2, 5 o 6
6 finale → stringa accettata
(a) -ad-> 2
-ac-> 1 -ac-> 3
0 \d->
-ab-> 4 -d-> 5
-d-> (6)
si parte dallo stato iniziale
le frecce indicano gli spostamenti ammessi
la prima a permette di raggiungere 1 o 4
(nota: non permette di restare in 0)
c'è un percorso per uno stato finale → stringa accettata
(a) -ad-> 2
-ac-> 1 -ac-> 3
0 \d->
-ab-> 4 -d-> 5
-d-> (6)
cc porta solo in 3
bc non porta da nessuna parte
in un automa non deterministico possono esserci anche scelte obbligate o inesistenti
non solo scelte multiple
una stringa porta a più stati
uno di questi finale → stringa accettata
automa: uguale, togliendo il vincolo
quintupla ⟨ I, S, s0, N, A ⟩
tutto uguale, ma N non ha il vincolo sulle terne
è N⊆S×I×S
stato attuale s → insieme di stati attuali SA
successivo(SA, i) = {s' | ⟨s,i,s'⟩∈N e s∈SA}
si applica successivo una volta per ogni carattere
stringa c1c2…cn-1cn:
successivo( successivo( … successivo( successivo({s0}, c1), c2), … cn-1), cn)
è un insieme di stati
uno di questi stati in A → stringa accettata
si applica a varie cose, oltre agli automi
in generale:
non determinismo = varie scelte possibili a ogni passo
esempio: il problema dei 150 cavalieri
forma generale di molti problemi:
non determinismo: formalizza la scelta
in questo caso:
se esiste una sequenza di scelte che porta a una soluzione, allora esiste una disposizione accettabile
su un ipotetico "computer non deterministico"
(che non esiste)
for cavaliere in range(0, 150):
posizione[cavaliere]=scelta(0, 1, ... , 149)
for c in range(0, 150):
for d in range(0, 150):
if rivali[c,d]:
if posizione[c]==(posizione[d]+1)%150:
return false;
return true;
come funziona?
scelta delle posizioni:
for cavaliere in range(0, 149):
posizione[cavaliere]=scelta(0, 1, ... , 149)
verifica:
for c in range(0, 149):
for d in range(0, 149):
…
scelte arbitrarie delle posizioni
esiste una sequenza di scelte che porta a una soluzione
⇓
la soluzione esiste
come per gli automi:
esiste percorso per stato finale ⇒ stringa accettata
i sistemi non deterministici non esistono nella realtà
si simulano con sistemi deterministici
vantaggio del non determinismo:
il nondeterminismo permette di codificare alcuni problemi complessi in modo semplice
li codifica, non li risolve
applicazione degli automi non deterministici
nel verificare una stringa, si possono presentare scelte
nota:
si sta parlando del modo che usano i programmi per vedere se una stringa collima con un'espressione regolare
es: come l'interprete Python esegue re.match() e re.finditer()
la stringa contiene due d: ridotto.doc
la prima d è parte di .*
la seconda è l'inizio di doc
ridotto.doc ↑-------↑↑↑ r .* doc
leggo i caratteri uno per volta:
ridotto.doc e r.*doc
solo con rid, due possibilità:
nemmeno con la o riesco a scegliere
si sceglie una delle due possibilità
ma ci si ricorda dell'altra
se va male, si prova l'altra
algoritmo semplicistico
si pone una scelta:
si verifica se almeno una scelta porta al successo
in questo caso: la seconda scelta
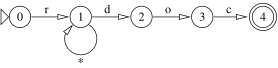
0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
esistono scelte: automa non deterministico
in 1 con carattere d:
stesso stato e carattere, ma due successori:
automa non deterministico

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
conversione manuale
esiste metodo per farlo automaticamente
in questo caso produce:
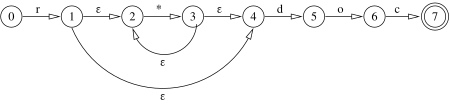
0 -r-> 1 -e-> 2 -.-> 3 -e-> 3 -d-> 4 -o-> 5 -c-> (6)
| ^ | ^
| +---e--+ |
+------e-------------+
archi ε = ci si può spostare senza caratteri

0 -r-> 1 -e-> 2 -*-> 3 -e-> 3 -d-> 4 -o-> 5 -c-> (6)
| ^ | ^
| +---e--+ |
+------e-------------+
quando si arriva in 1
prima che arrivi il prossimo carattere:
è una scelta non deterministica
non deterministiche:
anche entrambe le scelte in uno stato
arco ε e archi uscenti con carattere
modo automatico:
esempio…
((bd|c)a?)+
vogliamo l'automa
partiamo da quello che riconosce b da solo:
0 -b-> (1)
uno simile per a, per c e per d
poi: si compongono…
fatti: automi per b e per d
automa per bd:
0 -b-> 1 -e-> 2 -d-> (3)
volendo: eliminare arco ε
fondere i due stati in mezzo
abbiamo l'automa per bd
e quello per c
automa per bd|c:
-e-> 1 -b-> 2 -d-> 3 -e-> 0 (6) -e-> 4 -c--------> 5 -e->
sono i due messi in parallelo
collegati con archi ε
l'automa di a è come quello di b:
0 -a-> (1)
a? è a opzionale:
0 -a-> (1) -e->
arco ε da iniziale a finale
automi di bd|c e di a? noti
si concatenano e si ottiene quello di (bd|c)a?
ora: ripetizione non nulla di tutto
sarebbe il +
dato: automa di (bd|c)a?
automa di ((bd|c)a?)+:
-e-> 2 -b-> 3 -d-> 4 -e->
0 -e-> 1 7 -e-> 8 -a-> 9 -e-> (10)
-e-> 5 -c--------> 6 -e->
^ |
+---------------------e-------------------+
questo è l'automa di tutta l'espressione
-e-> 2 -b-> 3 -e-> 4 -d-> 5 -e->
0 -e-> 1 8 -e-> 9 -a-> 10 -e-> (11)
-e-> 6 -c---------------> 7 -e->
^ |
+---------------------e--------------------------+
perchè gli stati 0 e 11?
non si poteva iniziare con 1 e finire con 10?
per le ripetizioni non nulle servono i due stati aggiuntivi
altrimenti, l'automa di (a+b+)? accetterebbe aaa:
A* è uguale a (A+)?
automi di + e ?: visti sopra
si procede sempre nello stesso modo:
si ottiene un automa non deterministico
ora: convertirlo in deterministico
vale in generale
in particolare, anche per:
espressione regolare → automa non deterministico → deterministico
esempio…

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
dopo d è in 1 e 2
più stati insieme nello stesso momento
anche dopo

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
deterministico: in ogni momento un solo stato
non deterministico: più stati in ogni momento
(dato che ci sono le scelte)
idea: insieme_stati → stato
l'automa non deterministico si trova in ogni momento in un insieme di stati
per ogni insieme di stati, si crea uno stato nell'automa deterministico
più precisamente:
se successore può portare a un insieme di stati S, allora l'automa deterministico deve avere uno stato per S
frecce?
esempio:
ogni stato dell'automa deterministico simula un insieme di stati dell'automa non deterministico
le frecce sono di conseguenza
esiste un percorso verso uno stato finale
⇓
stringa accettata
quindi
gli stati finali dell'automa deterministico sono quelli che corrispondono a insiemi che contengono almeno uno stato finale dell'automa non deterministico
basta un solo stato finale a rendere finale l'intero insieme

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
in quali insiemi di stati può trovarsi?

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
da {0} solo in {1}
ma da 1 in 1 o in 2
quindi: stato {1,2}
ancora…

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
da {1,2} dove si va?
serve lo stato {1,3}

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
stessa cosa: c porta a {1,4}
d porta in {1,2}
tutti gli altri in 1

0 -r-> 1 -d-> 2 -o-> 3 -c-> (4)
(*)
d porta in 1 e in 2
tutti gli altri in 1
+---------------- -d ------------+
| +--------d----------+ |
(-d) V (d) V | |
{0} -r-> {1} -d-> {1,2} -o-> {1,3} -c-> ({1,4})
^ ^ -d-o| <-d- |-c
| +-------+ |-d
+---------------------+
-d = qualsiasi carattere tranne d
+---------------- -d ------------+
| +--------d----------+ |
(-d) V (d) V | |
{0} -r-> {1} -d-> {1,2} -o-> {1,3} -c-> ({1,4})
^ ^ -d-o| <-d- |-c
| +-------+ |-d
+---------------------+
stringa ridotto.doc
stringa accettata
























quelli visti finora finivano con:
ma si possono mettere anche più uscite
per automi accetta/rifiuta:
+----+
in ------+ SS |
+---+ +---+
| +----+ |
| |
+---------------+
| |
+--------------+ |
| |
| +-----+ | +-----+
+----+ MEM +------+-----+ ACC +----- out
+-----+ +-----+
uscita funzione dello stato
due reti ACC → due uscite
sul disegno:
stato → stato/uscita
in ogni stato si mette la sua uscita
stato con uscita: esempio
+-a-> 1/n -b-> 2/n -c-> 3/p | 0/n - qualsiasi_altro -> 7/n (*) | +-x-> 4/n -y-> 5/n -z-> 6/s
riconosce abc e xyz
non serve più mettere uno stato accettante
come nel caso normale
anche l'uscita va codificata in binario:
es: n=00, p=01, s=10
tabella stato → uscita
(stato: tre bit; uscita: due bit)
si trasforma in due circuiti con il sistema solito
uscite possibili:
uscite: 0, caffè, resto
------10c-----> ------10c-----> 4/r
0/0 -5c-> 1/0 -5c-> 2/0 -5c-> 3/c
-----10c----->
manca: ricomincia dall'inizio dopo l'erogazione
ingressi: 5c=0, 10c=1
stati: 000, …, 100
uscite: 0=00, c=01, r=10
tabella stato successivo:
| stato | ingresso | successivo |
|---|---|---|
| 000 | 0 | 001 |
| 000 | 1 | 010 |
| 001 | 0 | 010 |
| … |
uscite: 011→01, 100→10, altri 00