



The Butterfly is a robot consisting of a butterfly-shaped link (driven by an electrical motor) on whose rim a ball can freely roll. It was originally conceived by Kevin Lynch at Northwestern University, as an example of dynamic (i.e., nonprehensile) manipulation. Since the Butterfly is underactuated (two dof's – the link orientation and the ball position along the rim – and only one input), it brings up a number of interesting control problems. Two of them are discussed below.
The problem is to stabilize the system at a configuration where the butterfly link is horizontal and the ball is at one of the two associated unstable equilibria. The objective can be obtained via a two-phase controller. In the first phase (swing-up), a nonlinear energy-based control law drives the system to the heteroclinic trajectory which asymptotically approaches the desired equilibrium. In the second phase (balancing), an LQR control law keeps the system at the unstable configuration.
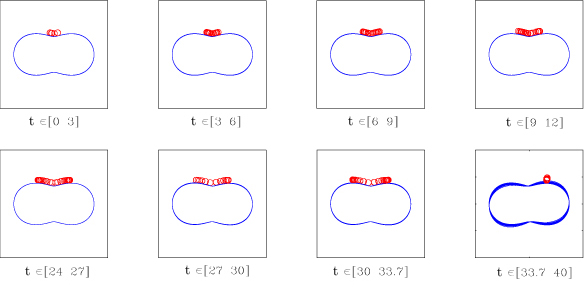
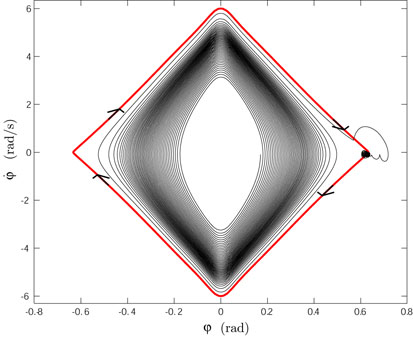
The above figure shows on the left the stroboscopic motion of the Butterfly, and on the right its trajectory in the ball phase plane (phi is the ball angular position along the link profile). The heteroclinic orbits (one for each unstable equilibrium) are marked in red. Note in the last part of the trajectory the effect of the LQR controller.
Watch here a simulation clip of the proposed controller. The simulation model is an accurate approximation of our experimental set-up, and includes various model perturbations such as friction and the effect of the ball angular velocity around its center (neglected for control design). Also simulated are an optical encoder for measuring the link orientation and a camera system providing the ball position, with the associated quantization and delay effects. The positive outcome of the simulation shows in particular that the energy-based approach, originally developed for conservative dynamics, can also work for dissipative systems.
